Significance
The stability of thin liquid films on solid surfaces is a topic of paramount importance in various engineering applications involving fluids at the nanoscale. This intriguing phenomenon has far-reaching implications, from nanomanufacturing of thin-film solar cells to the dynamics of tear films in the eye, and even the development of bionic nanodevices for regenerative medicine. As these liquid films become thinner, entering the realm of nanoscale heights, a host of physical effects that are often negligible at larger scales come into play. The interaction between molecules of the solid and the liquid becomes increasingly important and can lead to film rupture and subsequent dewetting of the solid surface.
In theoretical models, the destabilizing forces acting on thin liquid films are often described by a disjoining pressure (Π*) formula, where Π* = -A*/(6πh*^3), with A* representing the Hamaker constant associated with the solid-liquid-vapor system. Balancing this destabilizing disjoining pressure with the stabilizing surface tension (γ*) yields critical film thickness criteria for linear instability. Films must be thinner than a certain threshold (H*) to become linearly unstable, allowing unstable waves to form. This criterion was theoretically established, and early experiments seemed to confirm this “spinodal” regime of rupture. However, the intricacies of thin film stability became more apparent as researchers delved deeper into the subject. Novel experimental setups in the late 1990s focused on the breakup of ultrathin films, revealing different breakup morphologies and the influence of film/substrate defects in creating a “nucleation regime” of breakup. Computational models of thin films, augmented with disjoining pressure, were employed to rationalize these observations within the spinodal regime. Notably, these models highlighted the role of thermal fluctuations in both accelerating spinodal breakup and introducing a new “thermal regime” of breakup, even in initially linearly stable films. Thermal fluctuations, driven by thermal (Brownian) motion within the bulk of a liquid, create nanoscale waves at confining interfaces, known as nanowaves. Despite experimental evidence of this phenomenon, a comprehensive theoretical framework for understanding the “thermal regime” of thin film breakup, especially in the presence of large nanowaves, remained elusive.
To address this gap in understanding, new study published in the Journal Physical Review Fluids led by Professor James E. Sprittles, Jingbang Liu, Duncan A. Lockerby, and Associate Professor Tobias Grafke conducted molecular dynamics (MD) simulations, effectively creating a virtual nanoscale laboratory. In their simulations, they considered a quasi-2D geometry with periodicity enforced along one dimension. The system involved a thin film of Lennard-Jones liquid at low temperature, resting on a solid substrate. All intermolecular interactions were modeled using a Lennard-Jones potential, and the key parameter A* was determined.
Their simulations revealed a previously unexplored “thermal regime” of thin film rupture. This regime, characterized by the presence of large nanowaves, challenged conventional expectations and extended beyond the classical spinodal regime. Interestingly, the MD simulations also demonstrated that rupture within the thermal regime is a stochastic process, requiring statistical characterization. The rupture time and film profiles were recorded and analyzed, showing qualitative agreement with experimental observations. However, it is important to note that MD simulations, while powerful in capturing nanoscale physics, are computationally intensive, especially when dealing with larger, three-dimensional systems. To bridge the gap between MD simulations and macroscopic theory and to extend the framework to experimental scales, a more tractable approach was necessary.
The researchers turned to fluctuating hydrodynamics, a macroscopic theory that incorporates thermal fluctuations into fluid dynamics. Building on the work of Landau and Lifshitz, who introduced a “noisy” stress tensor to the Navier-Stokes equations, the team derived a stochastic thin-film equation (STF) for films on solid substrates. This STF, which describes the evolution of the film height, incorporates both surface tension and a disjoining pressure term. Incorporating thermal fluctuations, the STF allows for the prediction of thin film rupture beyond the limitations of MD simulations. The researchers conducted simulations using this STF, focusing on a quasi-2D scenario with periodic boundary conditions. The STF successfully reproduced the rupture phenomenon observed in MD simulations, providing valuable insights into the thermal regime.
Moreover, the STF framework offers the advantage of computational efficiency, allowing for the exploration of a broader parameter space and larger domain sizes. This paves the way for comparisons with experimental observations and practical applications.
The newly developed theoretical framework not only advances our understanding of thin liquid film stability at the nanoscale but also opens doors to experimental validation and application. By varying system parameters, such as domain size and film thickness, researchers can extend the predictions of the STF to experimental scales. Notably, the noise parameter ε, which characterizes the amplitude of thermal fluctuations, remains independent of system size. This implies that the framework can be scaled up to match experimental conditions. For instance, considering a domain size on the order of micrometers, the framework predicts rupture times that are well within the experimental range. This has significant implications for the stability of liquid coatings and other practical applications.
The theoretical framework developed in this study has far-reaching implications for understanding and predicting the behavior of fluids at the nanoscale, influenced by thermal fluctuations. Beyond thin film stability, researchers can explore various interfacial flows and free-boundary problems, including the dynamics of bubbles and drops in foams and emulsions, wetting layers, soap films, and even the stability of nanobubbles. The framework can also shed light on the role of fluctuations in phenomena such as wetting, superfluidity, and depinning transitions. Additionally, it has the potential to contribute to the understanding of nucleation and cavitation processes in bubbles and ice formation. As experimental techniques continue to advance, the framework can be used to interpret and predict results in a wide range of scenarios.
In theoretical models, the destabilizing forces acting on thin liquid films are often described by a disjoining pressure (Π*) formula, where Π* = -A*/(6πh*^3), with A* representing the Hamaker constant associated with the solid-liquid-vapor system. Balancing this destabilizing disjoining pressure with the stabilizing surface tension (γ*) yields critical film thickness criteria for linear instability. Films must be thinner than a certain threshold (H*) to become linearly unstable, allowing unstable waves to form. This criterion was theoretically established, and early experiments seemed to confirm this “spinodal” regime of rupture. However, the intricacies of thin film stability became more apparent as researchers delved deeper into the subject. Novel experimental setups in the late 1990s focused on the breakup of ultrathin films, revealing different breakup morphologies and the influence of film/substrate defects in creating a “nucleation regime” of breakup. Computational models of thin films, augmented with disjoining pressure, were employed to rationalize these observations within the spinodal regime. Notably, these models highlighted the role of thermal fluctuations in both accelerating spinodal breakup and introducing a new “thermal regime” of breakup, even in initially linearly stable films. Thermal fluctuations, driven by thermal (Brownian) motion within the bulk of a liquid, create nanoscale waves at confining interfaces, known as nanowaves. Despite experimental evidence of this phenomenon, a comprehensive theoretical framework for understanding the “thermal regime” of thin film breakup, especially in the presence of large nanowaves, remained elusive.
To address this gap in understanding, new study published in the Journal Physical Review Fluids led by Professor James E. Sprittles, Jingbang Liu, Duncan A. Lockerby, and Associate Professor Tobias Grafke conducted molecular dynamics (MD) simulations, effectively creating a virtual nanoscale laboratory. In their simulations, they considered a quasi-2D geometry with periodicity enforced along one dimension. The system involved a thin film of Lennard-Jones liquid at low temperature, resting on a solid substrate. All intermolecular interactions were modeled using a Lennard-Jones potential, and the key parameter A* was determined.
Their simulations revealed a previously unexplored “thermal regime” of thin film rupture. This regime, characterized by the presence of large nanowaves, challenged conventional expectations and extended beyond the classical spinodal regime. Interestingly, the MD simulations also demonstrated that rupture within the thermal regime is a stochastic process, requiring statistical characterization. The rupture time and film profiles were recorded and analyzed, showing qualitative agreement with experimental observations. However, it is important to note that MD simulations, while powerful in capturing nanoscale physics, are computationally intensive, especially when dealing with larger, three-dimensional systems. To bridge the gap between MD simulations and macroscopic theory and to extend the framework to experimental scales, a more tractable approach was necessary.
The researchers turned to fluctuating hydrodynamics, a macroscopic theory that incorporates thermal fluctuations into fluid dynamics. Building on the work of Landau and Lifshitz, who introduced a “noisy” stress tensor to the Navier-Stokes equations, the team derived a stochastic thin-film equation (STF) for films on solid substrates. This STF, which describes the evolution of the film height, incorporates both surface tension and a disjoining pressure term. Incorporating thermal fluctuations, the STF allows for the prediction of thin film rupture beyond the limitations of MD simulations. The researchers conducted simulations using this STF, focusing on a quasi-2D scenario with periodic boundary conditions. The STF successfully reproduced the rupture phenomenon observed in MD simulations, providing valuable insights into the thermal regime.
Moreover, the STF framework offers the advantage of computational efficiency, allowing for the exploration of a broader parameter space and larger domain sizes. This paves the way for comparisons with experimental observations and practical applications.
The newly developed theoretical framework not only advances our understanding of thin liquid film stability at the nanoscale but also opens doors to experimental validation and application. By varying system parameters, such as domain size and film thickness, researchers can extend the predictions of the STF to experimental scales. Notably, the noise parameter ε, which characterizes the amplitude of thermal fluctuations, remains independent of system size. This implies that the framework can be scaled up to match experimental conditions. For instance, considering a domain size on the order of micrometers, the framework predicts rupture times that are well within the experimental range. This has significant implications for the stability of liquid coatings and other practical applications.
The theoretical framework developed in this study has far-reaching implications for understanding and predicting the behavior of fluids at the nanoscale, influenced by thermal fluctuations. Beyond thin film stability, researchers can explore various interfacial flows and free-boundary problems, including the dynamics of bubbles and drops in foams and emulsions, wetting layers, soap films, and even the stability of nanobubbles. The framework can also shed light on the role of fluctuations in phenomena such as wetting, superfluidity, and depinning transitions. Additionally, it has the potential to contribute to the understanding of nucleation and cavitation processes in bubbles and ice formation. As experimental techniques continue to advance, the framework can be used to interpret and predict results in a wide range of scenarios.
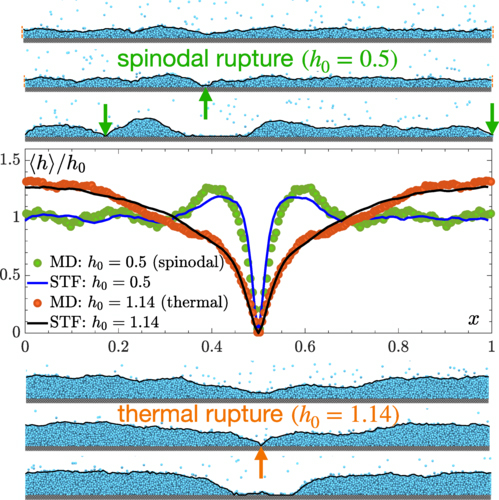
Image credit: Journal Physical Review Fluids, 2023

About the author
Professor James Sprittles
University of Warwick
University of Warwick

About the author
Dr. Tobias Grafke
Associate Professor
University of Warwick
Research Interests:
My research focuses on the development of numerical methods and mathematical tools to analyse stochastic systems. Applications include fluid dynamics and turbulence, atmosphere and ocean dynamics, and biological and chemical systems. My work concentrates on the prediction of pathways and rates of occurrence of rare and extreme events in realistic complex systems, to develop numerical methods for their simulation, and to quantify the effects of random perturbations on the system’s long term behavior.
Associate Professor
University of Warwick
Research Interests:
My research focuses on the development of numerical methods and mathematical tools to analyse stochastic systems. Applications include fluid dynamics and turbulence, atmosphere and ocean dynamics, and biological and chemical systems. My work concentrates on the prediction of pathways and rates of occurrence of rare and extreme events in realistic complex systems, to develop numerical methods for their simulation, and to quantify the effects of random perturbations on the system’s long term behavior.
Reference
James E. Sprittles, Jingbang Liu, Duncan A. Lockerby, and Tobias Grafke. Rogue nanowaves: A route to film rupture. Phys. Rev. Fluids 8, L092001 – Published 11 September 2023
Go to Phys. Rev. Fluids
